Посібник для ґіків з експериментів у машинному навчанні

Таблиця посилань

Анотація та 1. Вступ

1.1 Пост-хок пояснення

1.2 Проблема розбіжностей

1.3 Заохочення консенсусу пояснень

1. Пов'язані роботи

2. Pear: регуляризатор узгодження пост-хок пояснювача

3. Ефективність навчання консенсусу

   4.1 Метрики узгодження

   4.2 Покращення метрик консенсусу

   [4.3 Узгодженість за яку ціну?]()

   4.4 Чи все ще цінні пояснення?

   4.5 Консенсус та лінійність

   4.6 Два терміни втрат

4. Обговорення

   5.1 Майбутня робота

   5.2 Висновок, подяки та посилання

Додаток

A ДОДАТОК

A.1 Набори даних

У наших експериментах ми використовуємо табличні набори даних, спочатку з OpenML та скомпільовані в набір еталонних наборів даних від команди Inria-Soda на HuggingFace [11]. Ми надаємо деякі деталі про кожен набір даних:

\ Bank Marketing Це набір даних бінарної класифікації з шістьма вхідними ознаками і приблизно збалансованими класами. Ми навчаємо на 7 933 навчальних зразках і тестуємо на решті 2 645 зразках.

\ California Housing Це набір даних бінарної класифікації з сімома вхідними ознаками і приблизно збалансованими класами. Ми навчаємо на 15 475 навчальних зразках і тестуємо на решті 5 159 зразках.

\ Electricity Це набір даних бінарної класифікації з сімома вхідними ознаками і приблизно збалансованими класами. Ми навчаємо на 28 855 навчальних зразках і тестуємо на решті 9 619 зразках.

A.2 Гіперпараметри

Багато наших гіперпараметрів є постійними у всіх наших експериментах. Наприклад, всі MLP навчаються з розміром пакету 64 і початковою швидкістю навчання 0,0005. Також, всі MLP, які ми вивчаємо, мають 3 прихованих шари по 100 нейронів кожен. Ми завжди використовуємо оптимізатор AdamW [19]. Кількість епох варіюється від випадку до випадку. Для всіх трьох наборів даних ми навчаємо протягом 30 епох, коли 𝜆 ∈ {0,0, 0,25}, і 50 епох в інших випадках. При навчанні лінійних моделей ми використовуємо 10 епох і початкову швидкість навчання 0,1.

A.3 Метрики розбіжностей

Ми визначаємо кожну з шести метрик узгодження, використаних у нашій роботі.

\ Перші чотири метрики залежать від топ-𝑘 найважливіших ознак у кожному поясненні. Нехай 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) представляє топ-𝑘 найважливіших ознак у поясненні 𝐸, нехай 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) буде рангом важливості ознаки 𝑠 у поясненні 𝐸, і нехай 𝑠𝑖𝑔𝑛(𝐸, 𝑠) буде знаком (позитивним, негативним або нульовим) оцінки важливості ознаки 𝑠 у поясненні 𝐸.

\

\ Наступні дві метрики узгодження залежать від усіх ознак у кожному поясненні, а не лише від топ-𝑘. Нехай 𝑅 буде функцією, яка обчислює ранжування ознак у поясненні за важливістю.

\

\ (Примітка: Krishna та ін. [15] вказують у своїй статті, що 𝐹 має бути набором ознак, визначених кінцевим користувачем, але в наших експериментах ми використовуємо всі ознаки з цією метрикою).

A.4 Результати експерименту з непотрібними ознаками

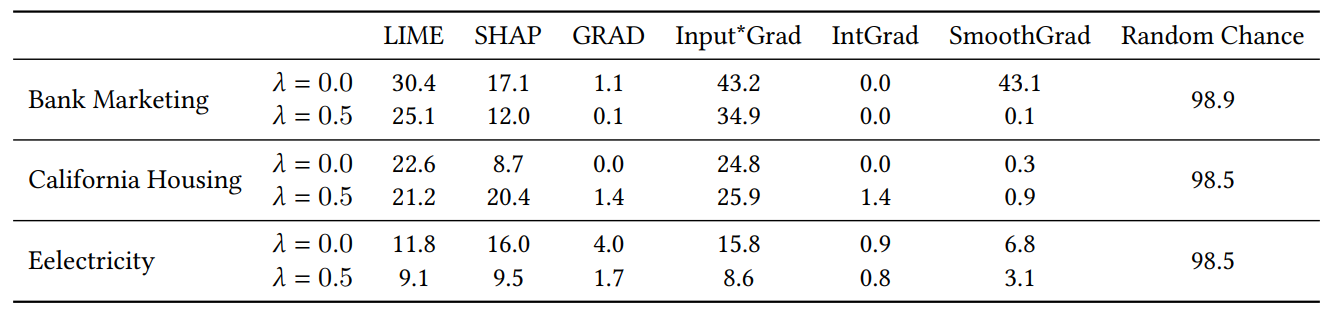
Коли ми додаємо випадкові ознаки для експерименту в розділі 4.4, ми подвоюємо кількість ознак. Ми робимо це, щоб перевірити, чи пошкоджує наша втрата консенсусу якість пояснення, розміщуючи нерелевантні ознаки в топ-𝐾 частіше, ніж моделі, навчені природним шляхом. У таблиці 1 ми повідомляємо відсоток випадків, коли кожен пояснювач включав одну з випадкових ознак у топ-5 найважливіших ознак. Ми спостерігаємо, що в цілому ми не бачимо систематичного збільшення цих відсотків між 𝜆 = 0,0 (базова MLP без нашої втрати консенсусу) і 𝜆 = 0,5 (MLP, навчена з нашою втратою консенсусу)

\

A.5 Більше матриць розбіжностей

\

\

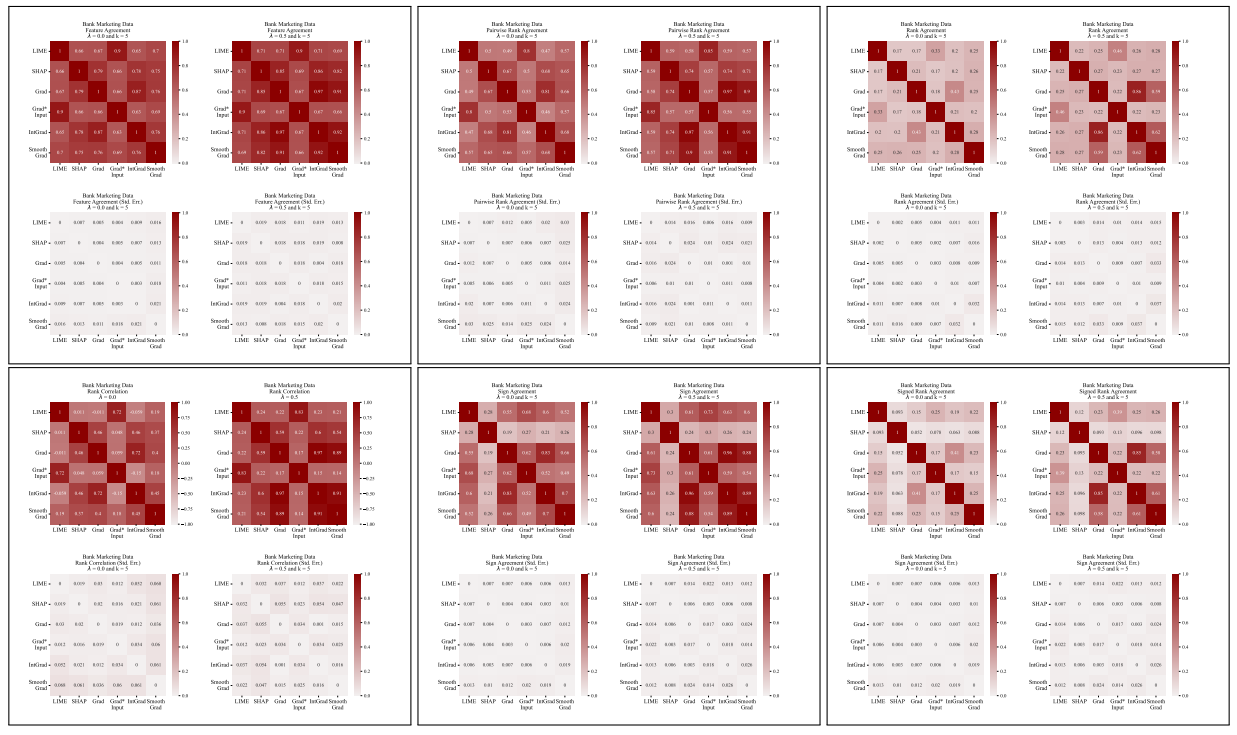
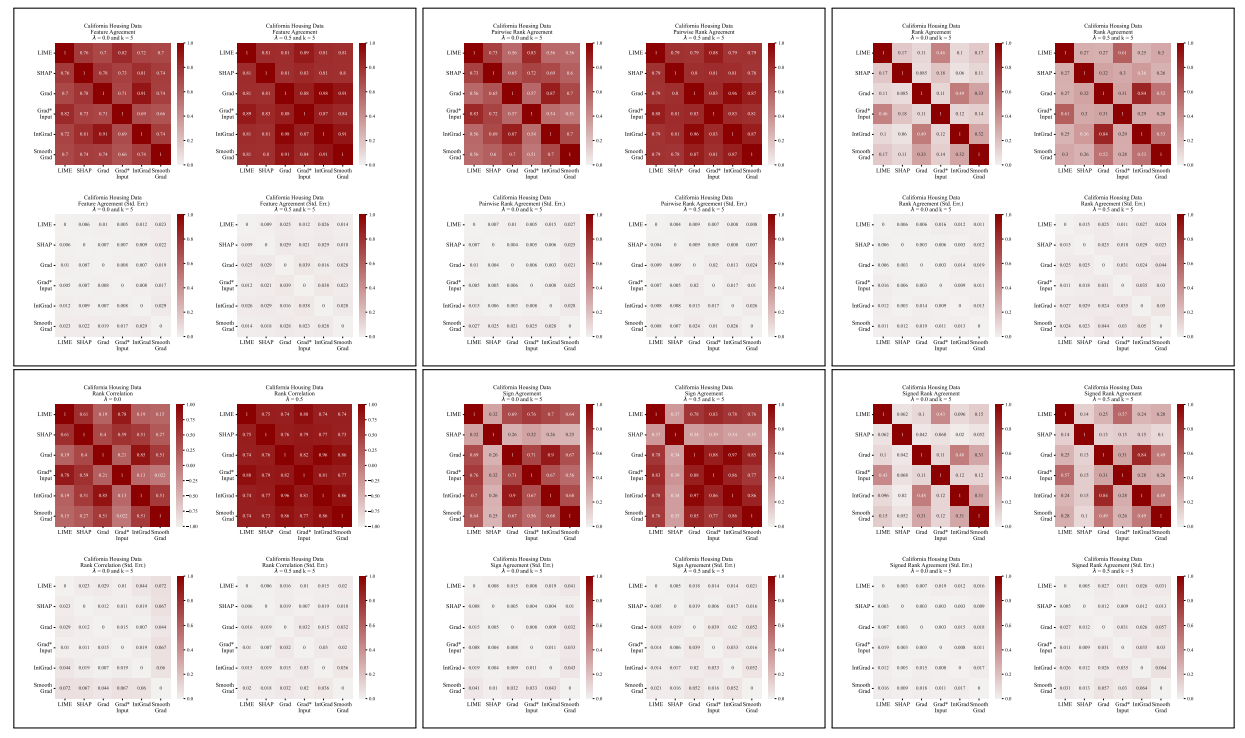
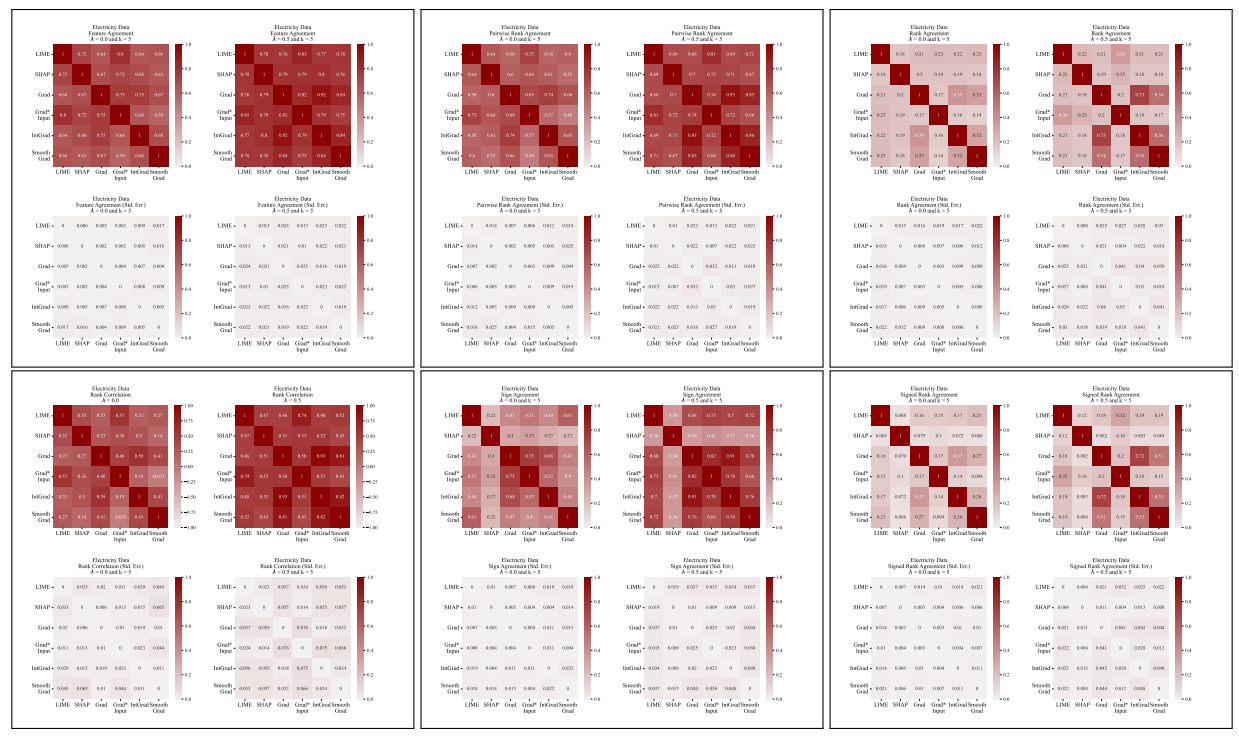
A.6 Розширені результати

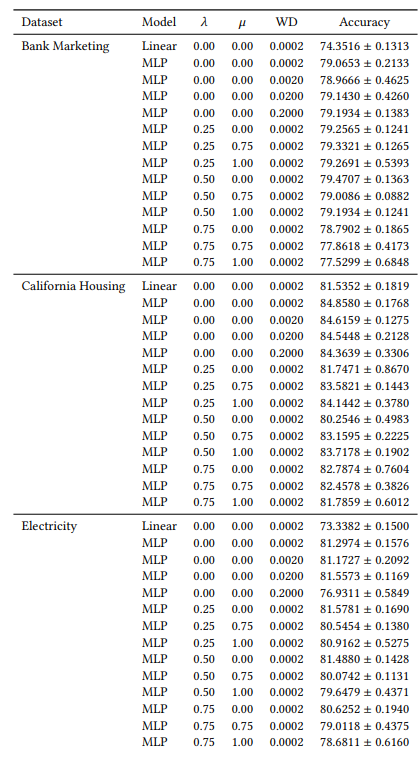
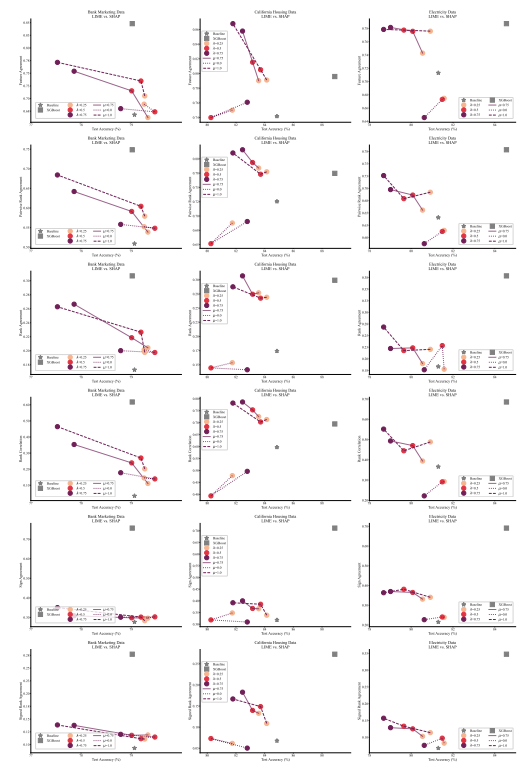
A.7 Додаткові графіки

\

\

\

\

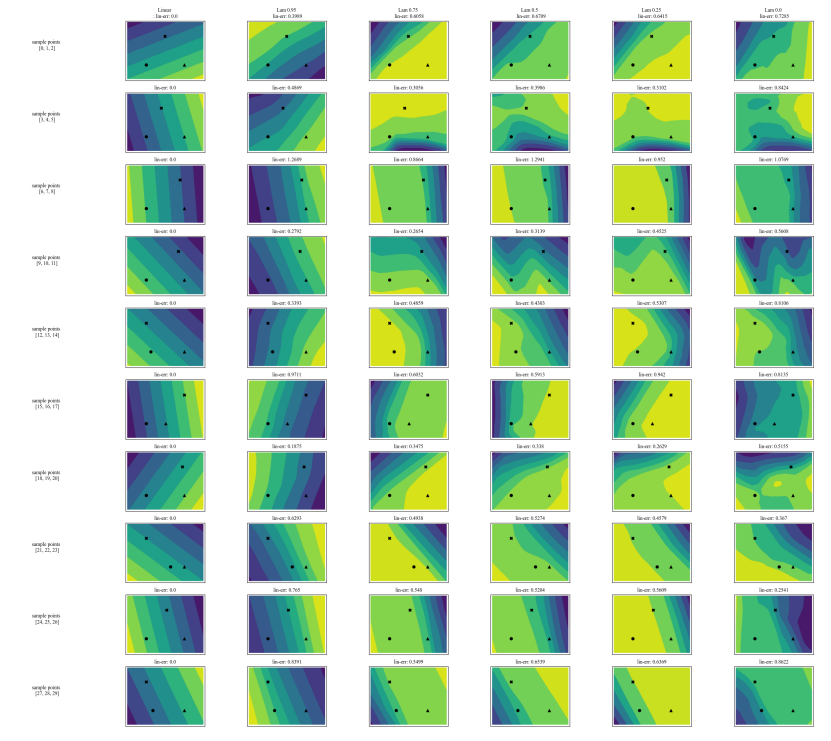
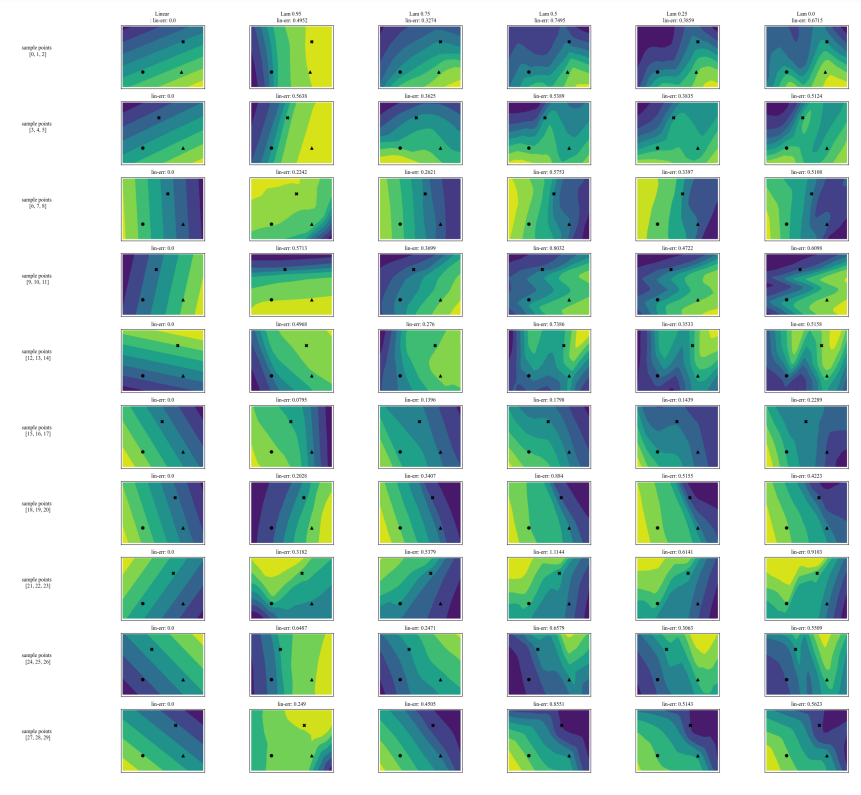
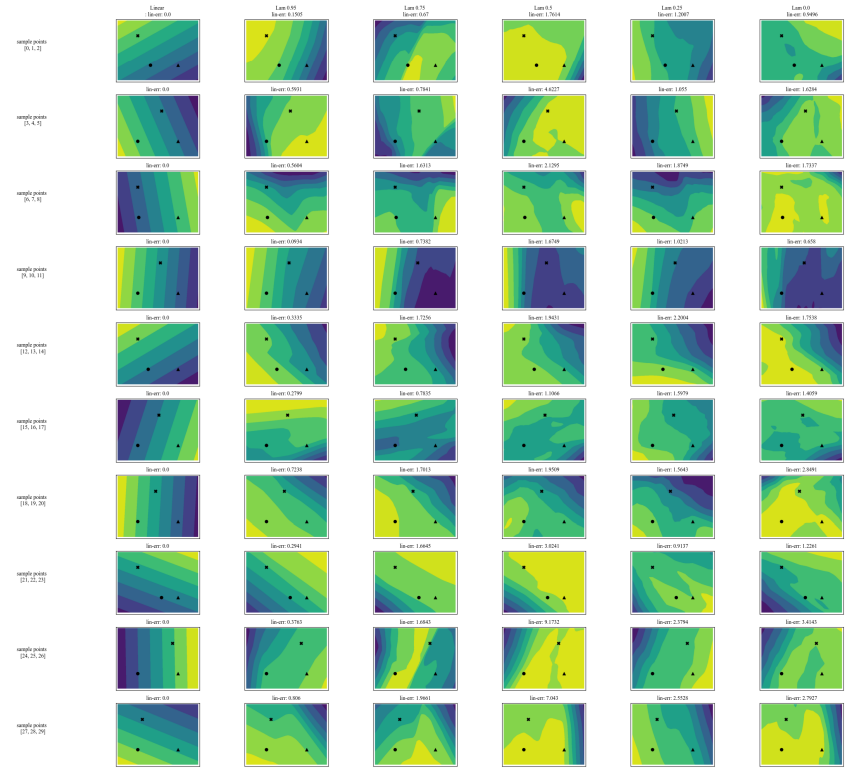
:::info Автори:

(1) Аві Шварцшильд, Університет Меріленду, Коледж-Парк, Меріленд, США та робота завершена під час роботи в Arthur (avi1umd.edu);

(2) Макс Цембалест, Arthur, Нью-Йорк, Нью-Йорк, США;

(3) Картік Рао, Arthur, Нью-Йорк, Нью-Йорк, США;

(4) Кіган Хайнс, Arthur, Нью-Йорк, Нью-Йорк, США;

(5) Джон Дікерсон†, Arthur, Нью-Йорк, Нью-Йорк, США ([email protected]).

:::

:::info Ця стаття доступна на arxiv за ліцензією CC BY 4.0 DEED.

:::

\